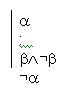Dedução Natural: Alexandre, Liège e Danilo
Lihkluppel (disc | contribs) |
Lihkluppel (disc | contribs) |
||
| (12 edições intermediárias de um usuário não apresentadas) | |||
| Linha 4: | Linha 4: | ||
| − | + | ||
| − | + | ||
| + | == Motivação == | ||
| + | |||
O sistema de dedução natural surgiu a partir da insatisfação reinante com relação aos sistemas de demonstração formal existentes anteriormente, que foram criados por Hilbert, Frege, e Russell. Jaśkowski começou, em 1929, a desenvolver um sistema dedutivo mais natural, utilizando-se de uma notação diagramática e, posteriormente atualizando sua proposta em meados dos anos 30. Porém, a forma moderna da dedução natural foi proposta por G. Gentzen, um matemático alemão, em uma dissertação entregue à faculdade de ciências matemáticas da universidade de Göttingen, no ano de 1935. Gentzen foi motivado pelo desejo de estabilizar a consistência da teoria dos números. Ele encontrou, rapidamente, uso para seu cálculo de dedução natural, mas ficou descontente com a complexidade de suas demonstrações, e em 1938 deu uma nova consistência as suas demonstrações. | O sistema de dedução natural surgiu a partir da insatisfação reinante com relação aos sistemas de demonstração formal existentes anteriormente, que foram criados por Hilbert, Frege, e Russell. Jaśkowski começou, em 1929, a desenvolver um sistema dedutivo mais natural, utilizando-se de uma notação diagramática e, posteriormente atualizando sua proposta em meados dos anos 30. Porém, a forma moderna da dedução natural foi proposta por G. Gentzen, um matemático alemão, em uma dissertação entregue à faculdade de ciências matemáticas da universidade de Göttingen, no ano de 1935. Gentzen foi motivado pelo desejo de estabilizar a consistência da teoria dos números. Ele encontrou, rapidamente, uso para seu cálculo de dedução natural, mas ficou descontente com a complexidade de suas demonstrações, e em 1938 deu uma nova consistência as suas demonstrações. | ||
| Linha 11: | Linha 13: | ||
| − | + | ||
| − | + | == O Método == | |
| + | |||
Uma dedução é construída da seguinte maneira: primeiro, faz-se uma lista das premissas que estão a dispor, colocando-se uma em cada linha, e escrevendo “P” ao lado, para indicar que se trata de uma premissa. Cada linha em uma derivação é numerada e deve-se ter uma “justificativa” para a fórmula que nela se encontra. Feito isto, aplica-se alguma regra de inferência que permita acrescentar uma nova linha a essa derivação, contendo uma fórmula que é o resultado da aplicação da regra a fórmulas anteriores. | Uma dedução é construída da seguinte maneira: primeiro, faz-se uma lista das premissas que estão a dispor, colocando-se uma em cada linha, e escrevendo “P” ao lado, para indicar que se trata de uma premissa. Cada linha em uma derivação é numerada e deve-se ter uma “justificativa” para a fórmula que nela se encontra. Feito isto, aplica-se alguma regra de inferência que permita acrescentar uma nova linha a essa derivação, contendo uma fórmula que é o resultado da aplicação da regra a fórmulas anteriores. | ||
| Linha 18: | Linha 21: | ||
| − | + | ||
| − | + | == Regras de Inferência == | |
| + | |||
Em princípio, não há um limite quanto ao número de regras que se pode ter em um sistema. Há, naturalmente, um mínimo necessário – o conjunto de regras deve ser completo, isto é, idealmente elas devem ser capazes de mostrar a validade de todas as formas de argumento –, tendo, para cada operador, duas regras: uma que introduza o operador (ou seja, cujo resultado seja uma fórmula cujo símbolo principal é aquele operador), e uma que elimine o operador (ou seja, que, tomando como entrada uma fórmula cujo símbolo principal seja o operador, dê como resultado uma fórmula mais simples, de onde o operador tenha sido eliminado). De modo similar, para os quantificadores. | Em princípio, não há um limite quanto ao número de regras que se pode ter em um sistema. Há, naturalmente, um mínimo necessário – o conjunto de regras deve ser completo, isto é, idealmente elas devem ser capazes de mostrar a validade de todas as formas de argumento –, tendo, para cada operador, duas regras: uma que introduza o operador (ou seja, cujo resultado seja uma fórmula cujo símbolo principal é aquele operador), e uma que elimine o operador (ou seja, que, tomando como entrada uma fórmula cujo símbolo principal seja o operador, dê como resultado uma fórmula mais simples, de onde o operador tenha sido eliminado). De modo similar, para os quantificadores. | ||
| Linha 25: | Linha 29: | ||
| − | + | === Regras de Inferência Diretas === | |
Exemplos: | Exemplos: | ||
| Linha 32: | Linha 36: | ||
| − | + | === Regras de Inferência Hipotéticas === | |
O conjunto anterior de regras de inferência permite demonstrar a validade de um grande número de argumentos. Contudo, esse conjunto de regras não é completo, pois existem formas de argumento que são válidas no CQC (cálculo quantificacional clássico, o cálculo de predicados de primeira ordem), mas cuja validade não pode ser demonstrada apenas com essas regras. Em primeiro lugar, ainda faltam regras para os quantificadores. Em segundo lugar, foram mostradas apenas oito regras – quando se deveria ter ao menos dez (duas para cada operador). Este tópico tratará das regras para operadores que ainda faltam. Elas se diferenciam das regras diretas do tópico anterior por exigirem o uso de hipóteses. | O conjunto anterior de regras de inferência permite demonstrar a validade de um grande número de argumentos. Contudo, esse conjunto de regras não é completo, pois existem formas de argumento que são válidas no CQC (cálculo quantificacional clássico, o cálculo de predicados de primeira ordem), mas cuja validade não pode ser demonstrada apenas com essas regras. Em primeiro lugar, ainda faltam regras para os quantificadores. Em segundo lugar, foram mostradas apenas oito regras – quando se deveria ter ao menos dez (duas para cada operador). Este tópico tratará das regras para operadores que ainda faltam. Elas se diferenciam das regras diretas do tópico anterior por exigirem o uso de hipóteses. | ||
| − | + | ==== Regra de Prova Condicional (RPC)==== | |
[[Imagem:regra2.jpeg]] | [[Imagem:regra2.jpeg]] | ||
| − | Isto é, se, a partir de uma hipótese | + | Isto é, se, a partir de uma hipótese <math>\alpha</math> se deriva uma fórmula <math>\beta</math>, então se pode descartar <math>\alpha</math> e introduzir <math>\alpha</math><math>\rightarrow</math><math>\beta</math> na derivação. |
| − | + | ==== Regra de Redução ao Absurdo (RAA)==== | |
[[Imagem:regra3.jpeg]] | [[Imagem:regra3.jpeg]] | ||
| − | Isto é, se, a partir de uma hipótese | + | Isto é, se, a partir de uma hipótese <math>\alpha</math>, uma contradição <math>\beta</math><math>\wedge</math>¬<math>\beta</math> é derivada, então se pode descartar <math>\alpha</math> e introduzir ¬<math>\alpha</math> na derivação. |
| − | + | ==== O uso adequado das Regras de Inferência Hipotéticas ==== | |
| − | + | ||
'''I.''' Uma linha vertical deve ser introduzida na derivação toda vez que uma hipótese adicional for introduzida. | '''I.''' Uma linha vertical deve ser introduzida na derivação toda vez que uma hipótese adicional for introduzida. | ||
| Linha 60: | Linha 63: | ||
| − | + | === Regras Derivadas === | |
Regras derivadas, como o próprio nome diz, são regras que foram obtidas a partir das outras regras que já foram mostradas anteriormente. Regras derivadas servem para abreviar parte de uma dedução; tudo o que se pode fazer com elas pode também ser feito sem elas, usando-se apenas as regras iniciais. Assim, regras derivadas são regras de abreviação. | Regras derivadas, como o próprio nome diz, são regras que foram obtidas a partir das outras regras que já foram mostradas anteriormente. Regras derivadas servem para abreviar parte de uma dedução; tudo o que se pode fazer com elas pode também ser feito sem elas, usando-se apenas as regras iniciais. Assim, regras derivadas são regras de abreviação. | ||
| Linha 73: | Linha 76: | ||
| − | + | == Definições == | |
| − | + | ||
| − | '''Definição 1:''' Sejam <math>\Gamma</math> um conjunto qualquer de fórmulas e <math>\alpha</math> uma fórmula. Uma dedução de <math>\alpha</math> | + | '''Definição 1:''' Sejam <math>\Gamma</math> um conjunto qualquer de fórmulas e <math>\alpha</math> uma fórmula. Uma dedução de <math>\alpha</math> a partir de <math>\Gamma</math> é uma seqüência finita <math>\delta</math>1,...,<math>\delta</math>n de fórmulas, tal que <math>\delta</math>n = <math>\alpha</math> e cada <math>\delta</math>i, 1 < i < n, é uma fórmula que pertence a <math>\Gamma</math> ou foi obtida a partir de fórmulas que aparecem antes na seqüência, por meio da aplicação de alguma regra de inferência. |
| + | |||
| + | '''Definição 2:''' Sejam <math>\Gamma</math> um conjunto qualquer de fórmulas e <math>\alpha</math> uma fórmula. Diz-se que <math>\alpha</math> é conseqüência lógica (sintática) de <math>\Gamma</math>, o que se denota por ‘<math>\Gamma</math>├ <math>\alpha</math>’, se há uma dedução de <math>\alpha</math> a partir de <math>\Gamma</math>. | ||
| + | |||
| + | |||
| + | |||
| + | == Teoremas == | ||
| + | |||
| + | Semanticamente, na conseqüência lógica, existe um tipo especial de fórmula, as fórmulas válidas, que são aquelas verdadeiras em toda e qualquer estrutura. Alternativamente, elas podem ser definidas como aquelas fórmulas que são conseqüência lógica de um conjunto vazio de premissas. | ||
| + | |||
| + | Caracterizando conseqüência lógica de uma maneira sintática, como feito em dedução natural, obtêm-se algo similar: os teoremas. | ||
| + | |||
| + | |||
| + | '''Definição 3:''' Uma fórmula <math>\alpha</math> é um teorema (do CQC) se há uma dedução de <math>\alpha</math> a partir do conjunto vazio de premissas. | ||
| + | |||
| + | Assim, <math>\alpha</math> é um teorema do CQC se e somente se <math>\oslash</math>├ <math>\alpha</math>, o que se abrevia escrevendo simplesmente ├ <math>\alpha</math>. | ||
| + | |||
| + | |||
| + | |||
| + | == Conseqüência sintática e conseqüência semântica == | ||
| + | |||
| + | A definição semântica de conseqüência afirma que uma fórmula <math>\alpha</math> é conseqüência lógica (semântica) de um conjunto <math>\Gamma</math> de fórmulas se toda estrutura que for modelo de <math>\Gamma</math> é um modelo de <math>\alpha</math>, o que se indica por <math>\Gamma</math>╞ <math>\alpha</math>. | ||
| + | |||
| + | Já sintaticamente, um argumento é válido se sua conclusão puder ser produzida a partir das premissas por meio da aplicação de certas regras de inferência (dedução 2). | ||
| + | |||
| + | Tendo definidas as duas noções de conseqüência, pode-se mostrar que, no CQC, as duas noções coincidem. Isto é, <math>\alpha</math> é uma conseqüência sintática de <math>\Gamma</math> se e somente se <math>\alpha</math> é uma conseqüência semântica de <math>\Gamma</math>, o que vale dizer que o método de dedução natural é um sistema de prova correto e completo para o CQC. Correto porque se uma conclusão pode ser deduzida de um conjunto <math>\Gamma</math> de premissa, então ela de fato é conseqüência lógica de <math>\Gamma</math>. E completo porque, se uma fórmula é conseqüência lógica de um conjunto de premissas, há uma dedução demonstrando isso. Isso tudo é sintetizado no seguinte teorema (Teorema de Correção e Completude), onde <math>\Gamma</math> é um conjunto qualquer de fórmulas: | ||
| − | + | <math>\Gamma</math> ├ <math>\alpha</math> se e somente se <math>\Gamma</math>╞ <math>\alpha</math>. | |
Edição atual tal como 18h37min de 30 de março de 2009
Dedução natural é um dos sistemas dedutivos utilizados para construir demonstrações formais na Lógica. Tal sistema foi introduzido pela primeira vez na Lógica Clássica nos anos 30, por Gentzen e Jaśkowski. O método de dedução natural permite mostrar a validade de um argumento de uma maneira muito mais prática e compacta em relação ao método da tabela-verdade.
Basicamente, o procedimento consiste em aplicar um conjunto de regras de inferência ao conjunto de premissas, gerando conclusões intermediárias às quais aplicam-se novamente as regras, até atingir-se a conclusão final desejada. A esse processo dá-se o nome deduzir, derivar ou provar a conclusão a partir do conjunto das premissas, e a seu resultado, obviamente, uma dedução ou derivação ou prova.
Tabela de conteúdo |
Motivação
O sistema de dedução natural surgiu a partir da insatisfação reinante com relação aos sistemas de demonstração formal existentes anteriormente, que foram criados por Hilbert, Frege, e Russell. Jaśkowski começou, em 1929, a desenvolver um sistema dedutivo mais natural, utilizando-se de uma notação diagramática e, posteriormente atualizando sua proposta em meados dos anos 30. Porém, a forma moderna da dedução natural foi proposta por G. Gentzen, um matemático alemão, em uma dissertação entregue à faculdade de ciências matemáticas da universidade de Göttingen, no ano de 1935. Gentzen foi motivado pelo desejo de estabilizar a consistência da teoria dos números. Ele encontrou, rapidamente, uso para seu cálculo de dedução natural, mas ficou descontente com a complexidade de suas demonstrações, e em 1938 deu uma nova consistência as suas demonstrações.
Prawitz desenvolveu uma monografia em 1965 apresentando o sistema de dedução natural na forma mais conhecida nos dias de hoje, incluindo também aplicações para lógica modal e de segunda ordem.Ele se baseou bastante no trabalho de Gentzen.
O Método
Uma dedução é construída da seguinte maneira: primeiro, faz-se uma lista das premissas que estão a dispor, colocando-se uma em cada linha, e escrevendo “P” ao lado, para indicar que se trata de uma premissa. Cada linha em uma derivação é numerada e deve-se ter uma “justificativa” para a fórmula que nela se encontra. Feito isto, aplica-se alguma regra de inferência que permita acrescentar uma nova linha a essa derivação, contendo uma fórmula que é o resultado da aplicação da regra a fórmulas anteriores.
As regras básicas de inferência são postuladas (aceitas sem demonstração). Tais regras devem preservar a verdade: se as fórmulas às quais a regra se aplica são verdadeiras, a fórmula resultante também o será.
Regras de Inferência
Em princípio, não há um limite quanto ao número de regras que se pode ter em um sistema. Há, naturalmente, um mínimo necessário – o conjunto de regras deve ser completo, isto é, idealmente elas devem ser capazes de mostrar a validade de todas as formas de argumento –, tendo, para cada operador, duas regras: uma que introduza o operador (ou seja, cujo resultado seja uma fórmula cujo símbolo principal é aquele operador), e uma que elimine o operador (ou seja, que, tomando como entrada uma fórmula cujo símbolo principal seja o operador, dê como resultado uma fórmula mais simples, de onde o operador tenha sido eliminado). De modo similar, para os quantificadores.
Existe quatro tipos de regras de inferência: as diretas, as hipotéticas, as derivadas e as para quantificadores.
Regras de Inferência Diretas
Exemplos:
Regras de Inferência Hipotéticas
O conjunto anterior de regras de inferência permite demonstrar a validade de um grande número de argumentos. Contudo, esse conjunto de regras não é completo, pois existem formas de argumento que são válidas no CQC (cálculo quantificacional clássico, o cálculo de predicados de primeira ordem), mas cuja validade não pode ser demonstrada apenas com essas regras. Em primeiro lugar, ainda faltam regras para os quantificadores. Em segundo lugar, foram mostradas apenas oito regras – quando se deveria ter ao menos dez (duas para cada operador). Este tópico tratará das regras para operadores que ainda faltam. Elas se diferenciam das regras diretas do tópico anterior por exigirem o uso de hipóteses.
Regra de Prova Condicional (RPC)
Isto é, se, a partir de uma hipótese <math>\alpha</math> se deriva uma fórmula <math>\beta</math>, então se pode descartar <math>\alpha</math> e introduzir <math>\alpha</math><math>\rightarrow</math><math>\beta</math> na derivação.
Regra de Redução ao Absurdo (RAA)
Isto é, se, a partir de uma hipótese <math>\alpha</math>, uma contradição <math>\beta</math><math>\wedge</math>¬<math>\beta</math> é derivada, então se pode descartar <math>\alpha</math> e introduzir ¬<math>\alpha</math> na derivação.
O uso adequado das Regras de Inferência Hipotéticas
I. Uma linha vertical deve ser introduzida na derivação toda vez que uma hipótese adicional for introduzida.
II. Não deve ser usada uma fórmula que ocorre à direita de uma linha vertical depois de terminada esta linha.
III. As hipóteses devem ser descartadas na ordem inversa em que foram introduzidas.
IV. A dedução não termina enquanto não forem descartadas todas as hipóteses adicionadas.
Regras Derivadas
Regras derivadas, como o próprio nome diz, são regras que foram obtidas a partir das outras regras que já foram mostradas anteriormente. Regras derivadas servem para abreviar parte de uma dedução; tudo o que se pode fazer com elas pode também ser feito sem elas, usando-se apenas as regras iniciais. Assim, regras derivadas são regras de abreviação.
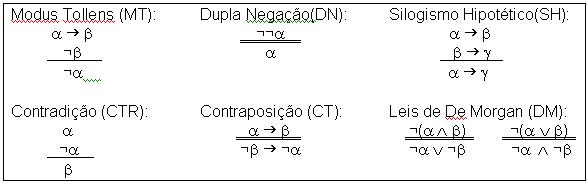
Exemplos:
Obs.: Os dois traços que separam a premissa da regra de sua conclusão em DN, CT e DM significa que são regras de inferência reversíveis: funcionam nas duas direções.
Existem, claro, outras regras derivadas. Na verdade, pode-se introduzir tantas regras derivadas quanto desejar, pois cada forma de argumento provada válida corresponde a uma regra. As regras derivadas usuais vão corresponder àquelas formas de argumento mais comumente empregadas, apenas isso. O que determina se uma regra é primitiva ou derivada é, basicamente, uma questão de convenção.
Definições
Definição 1: Sejam <math>\Gamma</math> um conjunto qualquer de fórmulas e <math>\alpha</math> uma fórmula. Uma dedução de <math>\alpha</math> a partir de <math>\Gamma</math> é uma seqüência finita <math>\delta</math>1,...,<math>\delta</math>n de fórmulas, tal que <math>\delta</math>n = <math>\alpha</math> e cada <math>\delta</math>i, 1 < i < n, é uma fórmula que pertence a <math>\Gamma</math> ou foi obtida a partir de fórmulas que aparecem antes na seqüência, por meio da aplicação de alguma regra de inferência.
Definição 2: Sejam <math>\Gamma</math> um conjunto qualquer de fórmulas e <math>\alpha</math> uma fórmula. Diz-se que <math>\alpha</math> é conseqüência lógica (sintática) de <math>\Gamma</math>, o que se denota por ‘<math>\Gamma</math>├ <math>\alpha</math>’, se há uma dedução de <math>\alpha</math> a partir de <math>\Gamma</math>.
Teoremas
Semanticamente, na conseqüência lógica, existe um tipo especial de fórmula, as fórmulas válidas, que são aquelas verdadeiras em toda e qualquer estrutura. Alternativamente, elas podem ser definidas como aquelas fórmulas que são conseqüência lógica de um conjunto vazio de premissas.
Caracterizando conseqüência lógica de uma maneira sintática, como feito em dedução natural, obtêm-se algo similar: os teoremas.
Definição 3: Uma fórmula <math>\alpha</math> é um teorema (do CQC) se há uma dedução de <math>\alpha</math> a partir do conjunto vazio de premissas.
Assim, <math>\alpha</math> é um teorema do CQC se e somente se <math>\oslash</math>├ <math>\alpha</math>, o que se abrevia escrevendo simplesmente ├ <math>\alpha</math>.
Conseqüência sintática e conseqüência semântica
A definição semântica de conseqüência afirma que uma fórmula <math>\alpha</math> é conseqüência lógica (semântica) de um conjunto <math>\Gamma</math> de fórmulas se toda estrutura que for modelo de <math>\Gamma</math> é um modelo de <math>\alpha</math>, o que se indica por <math>\Gamma</math>╞ <math>\alpha</math>.
Já sintaticamente, um argumento é válido se sua conclusão puder ser produzida a partir das premissas por meio da aplicação de certas regras de inferência (dedução 2).
Tendo definidas as duas noções de conseqüência, pode-se mostrar que, no CQC, as duas noções coincidem. Isto é, <math>\alpha</math> é uma conseqüência sintática de <math>\Gamma</math> se e somente se <math>\alpha</math> é uma conseqüência semântica de <math>\Gamma</math>, o que vale dizer que o método de dedução natural é um sistema de prova correto e completo para o CQC. Correto porque se uma conclusão pode ser deduzida de um conjunto <math>\Gamma</math> de premissa, então ela de fato é conseqüência lógica de <math>\Gamma</math>. E completo porque, se uma fórmula é conseqüência lógica de um conjunto de premissas, há uma dedução demonstrando isso. Isso tudo é sintetizado no seguinte teorema (Teorema de Correção e Completude), onde <math>\Gamma</math> é um conjunto qualquer de fórmulas:
<math>\Gamma</math> ├ <math>\alpha</math> se e somente se <math>\Gamma</math>╞ <math>\alpha</math>.